Chapter Five: Digital Audio

4. Sample Rates: The Nyquist Frequency and Aliasing

As mentioned in the Overview section, in 1928 a Swedish-born researcher for AT&T named Harry Nyquist published a paper entitled "Certain Topics in Telegraph Transmission Theory." In it, he presented a method for converting analog waveforms into digital signals for more accurate transmission over phone lines. If an analog signal were band-limited (i.e., had no frequencies higher than a specific band), it could be captured and transmitted in digital values and then recreated in an analog form on the receiving end. He presented the concept of sampling amplitudes at a specific rate, as described on the previous page. Most importantly, he determined that the sampling rate would need to be at least twice the highest frequency to be reproduced. Following Claude Shannon's mathematical proof in 1948, it became known as the Nyquist Theorem or the Nyquist-Shannon Theorem.

According to this theorem, the highest reproducible frequency of a digital system will be less than one-half the sampling rate. From the opposite point of view, the sampling rate must be greater than twice the highest frequency we wish to reproduce.* This frequency, half the sampling rate, is often called the Nyquist frequency. A hypothetical system sampling a waveform at 20,000 samples per second cannot reproduce frequencies above 10,000 Hz. It is important to note that this means all component frequencies, including higher partials of lower tones. Additionally, nasty things happen when a sampled frequency is exactly at the Nyquist frequency: often a zero amplitude signal will result. This is called the critical frequency.

The image below demonstrates a sine wave (in green) being sampled at four times its frequency, with an expected digital output similar to the blue step wave.

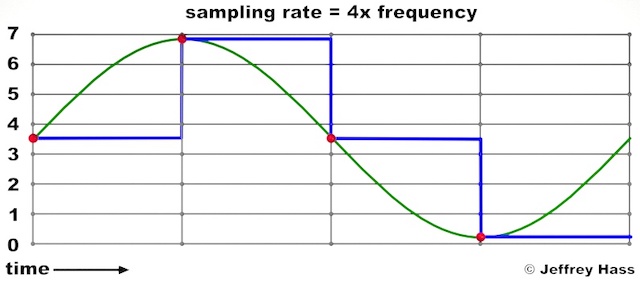
But what happens when a frequency above the Nyquist frequency is sampled and played back? Do these frequencies simply disappear? Unfortunately not. Frequencies above the Nyquist frequency cause aliasing (also sometimes called foldover or biasing). The spurious frequencies they produce are predictable, in that they are mirrored the same distance below the Nyquist frequency as the originals were above it, and at the original amplitudes. The higher the input frequency above the Nyquist frequency, the lower its output will actually sound when aliased.

The image below demonstrates a sine frequency input (in green) being sampled at slightly above its own frequency, not anywhere close to the over 2x's sample rate required to avoid aliasing. The blue step wave represents the sampled digital output, which will yield the orange sine wave output when smoothed out at the end of the process. The orange output sine wave is obviously way lower in frequency then the green input, as it has folded over or aliased. We will not hear the higher green sine wave output, only the orange one.

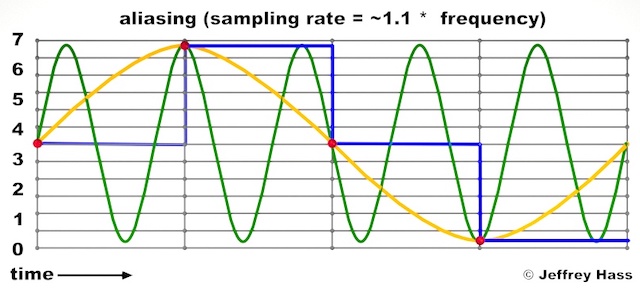
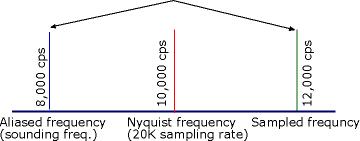
With an imaginary sampling rate of 20,000 samples per second (therefore a Nyquist frequency of 10,000 Hz), a frequency of 12,000 cps will alias at 8,000 cps, 2000 cps below the 10,000 cps Nyquist frequency, as pictured below. In the early day of low sampling rates, either one filtered input frequencies above the Nyquist frequency out, or one could hope these aliased frequencies were weak and would mirror back on other partials making them less noticeable. In the example below, this might be the case if the fundamental were 500, 1000, 2000 or 4000 cps, but not if it were 750,1500, 3000 or 6,000 Hz, which do not include the aliased tone in their spectra.

Particularly with digital synthesis and waveforms that were not band-limited, aliasing always seemed to be a possibility (I remember how easy it was, for example, to create aliasing with a Yamaha DX-7 and certain FM parameters). The band-limited pulse train waveform became extremely popular for buzzy sounds precisely because it was band-limited and could be calculated to stay below the Nyquist frequency.

The implication of the information above is that the sampling rate is responsible for the frequency response of the system.

Experiment: You can recreate a visual equivalent of aliasing in the following manner. Find a spinning ceiling fan. By altering the rate at which you blink, you should be able to create a false image of the fan blades moving more slowly or even moving backwards. A alternative method would be to watch an old Western, where the "sampling rate" of the film's frame rate creates an illusion of wagon wheels turning backwards, called temporal aliasing.

* The Nyquist theory, even as expressed here, is not exactly what Nyquist said. The accurate description is that the sampling frequency must be twice the bandwidth of the input signal. In audio, we normally include 0 Hz in the frequency band, making it a baseband signal (think lowpass range down to 0 Hz, rather than a bandpass range), so for our purposes the optimal audio bandwidth we wish to recreate is 0-20,000 Hz, so we may say that a sampling rate above 40,000 Hz will not cause aliasing.