Chapter Five: Digital Audio

6. Quantizing, Approximation Errors and Sample Size
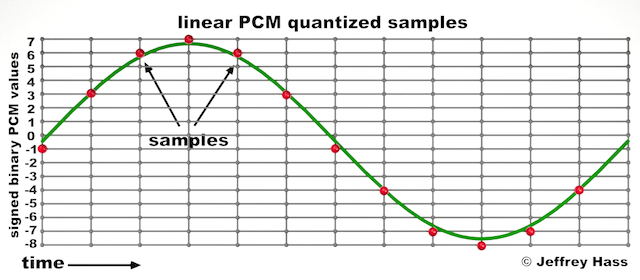
Samples, the periodic snapshots of the instantaneous amplitude of an input signal taken by the ADC, are assigned numeric values that the computer or digital circuit can use in a process called quantization. The number of available values which can be assigned is determined by the number of bits (0's and 1's) used for each sample, also called bit depth or bit resolution . Each additional bit doubles the number of values available (1-bit samples have 2 values, 2-bit samples have 4 values, etc.).
The most common form of uncompressed digital audio uses the pulse code modulation (PCM) system, mentioned earlier. PCM usually refers to linear PCM or LPCM, though it is usually just called PCM. In this system, as pictured below, the amplitude gradations are equally spaced from low amplitudes to high amplitudes, even though we hear logarithmically. For those using "do it yourself" digital synthesis programs like MAX, SuperCollider, Csound, etc., crescendos using linear amps, as they are called, have the perceptual quality of slowing down as they get louder, so it it quite common to use exponential envelopes instead. While common files formats like AIFF and WAV use linear PCM encoding, some, like A-law algorithm or the μ-law algorithm, vary with levels of amplitude.
When a sample is quantized, the instantaneous snapshot of its analog amplitude has to be rounded up or down (or simply truncated down in some systems) to the nearest available digital value. This rounding-off process is called approximation. The smaller the number of bits used per sample, the greater the numeric distance many of the analog values will need to be rounded off to the nearest digital value. The quantity difference between the analog value and the digital value is called the approximation error or quantizing error as shown in the illustration below as the red and green striped areas. The orange bars represent the quantized sample values.
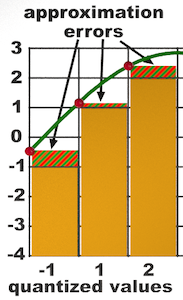
3-bit (8 values) samples
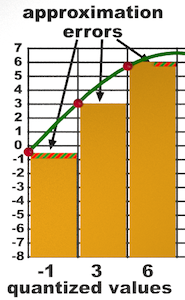
4-bit (16 values) samples
The image on the left has 8 values, the equivalent of a 3-bit sample size. The image on the right has 16 values, the equivalent of a 4-bit sample size. Notice how much smaller the approximation errors are on the right with double the number of values.
The greater the magnitude of approximation errors, the greater the level of digital or quantizing noise produced. The solution to reducing digital noise is to use larger sample word sizes (greater bit depth or precision), which therefore corresponds to the dynamic range of the system, since it affects the signal-to-noise ratio. For digital PCM systems, this is often measured as SQNR, or signal-to-quantization-noise-ratio which can be express in dB's. The SQNR can be calculated similarly to amplitude decibles as SQNR = 20 log10 (2# of bits) ≈ 6.02 * # of bits dB. Therefore, a general rule of thumb:
Every additional bit per sample size results in a ~6 dB greater dynamic range.
This makes sense if you read the section on decibels and amplitude, whereby a doubling of amplitude adds ~6 dB. Each additional bit per sample doubles the number of available values, and so the result is parallel. The original CD standard proposed by Sony was for a 14-bit sample size, with a dynamic range of only 84 dB, but was changed to 16 bits before inception.
Just as sample rate affects frequency response, sample size (i.e. bit depth) affects dynamic range, or the amplitude difference between the digital noise floor and the loudest possible sound before distortion. Sometimes its hard to wrap your head around how dynamic range is affected by the available number of binary values, so here is an extreme example. You can see the effect of two different bit depths in the diagrams below and how successfully they each represent the crescendo indicated by the green analog waveform being sampled. Notice that the one-bit sample depth doesn't have any dynamic change at all (yet they call that a 6 dB range—go figure).
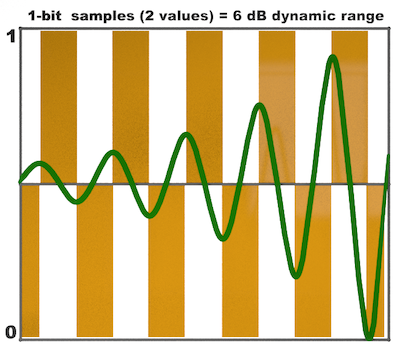
1-bit Samples (0 or 1)
With a 1-bit sample, there is no representation of a crescendo or increasing amplitude. The sound is either on or off, with large approximation errors at the lower amplitudes. It has a 6 dB dynamic range.
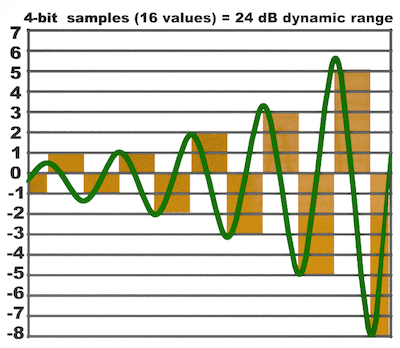
4-bit Samples (0000 to 1111)
With a 4-bit sample, the 16 available binary values approximate the crescendo much more successfully, and therefore has a greater dynamic range of 24 dB.
The CD standard of 16-bit samples, with its impressive 65,536 values for quantizing, provides the theoretical playback system optimum of a 96 dB dynamic range. However, for editing, many of the processes create fractional values that add to the approximation errors, so it is standard procedure to now to edit in 24-bit or higher resolution, with its 16,777,216 values and ~144 dB dynamic range. Additionally, as we constantly learn from the past, audio quality in the future will only improve, so keeping master copies of your works in 24-bits or higher is also recommended.
On the other end of the spectrum, chiptunes, which had a heyday in the 1980's as a result of video game music, deliberately used a low, 8-bit (48 dB SQNR) sample size, with only three music and one noise voice, to replicate the programmable sound processor (PSG) found on video consoles and arcade games. It is absolutely brilliant how the noise channel is used for percussion that masks the digital noise from the voice channels (and arpeggiation is used to compensate for the limited number of voices). The Super Mario Bros. theme would not sound quite the same in 16- or 24-bit resolution and unlimited polyphonic voices.