Appendices

Appendix D: Tuning and Temperament Intro for Electronic Musicians
Non-traditional tunings and temperaments for electronic musicians
Electronic music offers composers virtually limitless abilities to shape pitch structures and complex timbres as they see fit or avoid determinate pitches altogether. However, many composers see the use of non-traditional or extensions of historic tuning and temperament systems with synthesis as a liberating experience from the limitations of many Western orchestral instruments that simply cannot physically adapt to the myriad of tuning approaches out there. This short appendix aims to provide access to some of the vast material on the subject out there for further exploration for those interested in applying these concepts and methods.
Before reading further, a review of the harmonic series is recommended if needed. We expect nature to often be perfect, but in attempting to bend it to our compositional will, certain adjustments to tuning systems are often employed. These adjustments, whether modern or historic, are referred to as temperaments. Perhaps the most well-known of these is 12-tone equal temperament (12TET or 12 EDO, for equidistant division of the octave) in which all half-steps are an equivalent 100 cents, summing to 1200 cents per octave. Identical intervals and chords, regardless of their scalar placement, are equivalent, and all intervals, aside from the octave, diverge from their natural “pure” harmonic equivalents (for example, the perfect 5th between partial 2 and partial 3 which is 2 cents narrower in ET). In other words, when compared to the harmonic series, they are all “out of tune” (explained below), but allow for complete tonal mobility with equal results.
The image below shows the first 20 harmonic partials of C (remember the fundamental is partial #1). Above are the number of cents the pure harmonic differs from ET. Blue and red notes indicate particularly flat or sharp pitch deviations respectively.
Just Intonation and Just Intervals
Just intonation (JI), in most of its forms, is the tuning of notes based on whole number ratios, primarily pertaining to the harmonic series of a particular fundamental root key. It is not usually considered a temperament, which implies certain adjustments are made to fit tonal needs. It is customary to reduce these just ratios to their octave equivalent, so an octave with a ratio of 2:1 can be reduced to 1:1. Since higher partials of a fundamental are multiples of that base frequency, certain strong relationships can exist. A “pure” or “just” fifth would be the ratio between the 2nd and 3rd partial, and conventionally named would be a ratio of 3:2, so one may multiply the frequency of the lower note with this ratio and obtain the upper note. In this way, a just 4th would be 4:3 and a just major 3rd would be 5:4.
Different historic and modern tuning systems make various adjustments to an octave that differ from a pure just intonation scale. Some of these systems use what are called limits. Pythagorean tuning, for example, uses 3-limit ratios. This means that the integers of the ratios are limited to a maximum of 3 and its powers. So, one can derive not only the 3:2 just 5th, but also a 9:4 just major 9th (by octave reduction, a major 2nd) and an 81:64 just major 3rd.
5-limit tuning allows for integer ratios using up to 5 and their powers, such as the just 5:4 major 3rd and the 15:8 major 7th. Comparing the 5- and 3-limit major 3rd produces a difference of 81:80, which is called the syntonic comma (more on commas below). Modern just limit systems may go up primes to 7-,11- and 13-limit with extremely high-numbered ratios.
THE CIRCLE OF FIFTHS IS MORE LIKE A SPIRAL
Most musicians are familiar with the Circle of Fifths. Its functions and relationships permeate tonal music and many tuning systems. As pictured below, if we travel forwards or backwards around the circle from any starting point, after 12 pitches, in either direction, we end up back on the pitch we started on. Or do we?
Pure fifths, described as “just” are derived from harmonic partials 3 and 2, are therefore in a ratio of 3/2 (for example, 150 Hz and 100 Hz). They share many strong harmonic partials, as shown below and therefore blend without beating amongst the strongest partials.
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | ... |
| 150 | 300 | 450 | 600 | 750 | 900 | 1050 | 1200 | 1350 | ... |
Pythagoras noted if you traveled around the Circle of Fifths by pure fifths, and adjusting via octave transposition, by the time you reached the starting point, the ending pitch was almost a quarter of a semi-tone sharper (approximately 23.46 cents) than the beginning pitch, and that difference is called the Pythagorean comma. In equal temperament, this error is divided equally between the pitches, so the ET fifths are narrowed by approximately 2 cents.
So, the Circle of Fifths in pure tuning is actually a spiral. The spiral can be continued up through double sharps and down through double flats (which is a form of Pythagorean tuning) and beyond.
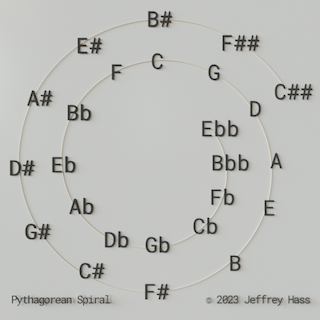
Many famous tunings are based on this phenomenon and may generate 31 tones or more. Pythagorean tuning for a traditional keyboard, with its limited number of keys, provides a large number of pure 5ths except for one by tuning 3 pure 5ths down on the flat side (from C to Eb, for example), and 8 pure 5ths up on the sharp side (from C to G#, for example). This leaves one nasty, “unpure” 5th between G# and Eb, which is narrow by one Pythagorean comma, or approximately a ¼ of a semitone, and may be placed tonally where it would least likely be used. It is aptly called the wolf.
Another system based on just intonation is the highly popular Renaissance and Baroque mean-tone tuning, where the pure major third, at a ratio of 5/4 (for the 5th and 4th partials) is the basis. Other intervals, such as the fifth are tempered. The just major third is ~386 cents wide compared to 12TET’s 400 cents. The errors based on mean-tone tunings are usually tempered, such as quarter-comma meantone, with 8 pure major thirds, but usually containing one very wide error or the same error divided between two intervals. Historic and modern extensions of meantone tuning include systems devised by Vicentino (31-tones), Huygens, Zarlino, Helmholtz and more modern 20th C. Adriaan Fokker (Fokker blocks), who also further developed 31-tone temperament. Both historic (Vicentino) and modern (Fokker) 31-tone keyboard instruments have been built.
Harry Partch, Ben Johnson (Partch’s student), Lou Harrison, James Tenney, Easley Blackwood, Kyle Gann (Johnson’s student) and so many more, have extended both theory and practice of just intonation principles of composition. Johnson even developed a notational system to get around the limitations of microtonal tunings and prime limits represented on a limited musical staff system. Partch, of course, designed acoustic instruments that fit his tuning systems, such as a 43-tone marimba. In electronics, Wendy Carlos developed a system of rapidly transposing the root key of a tuning system with a second keyboard.
In the microtonal community, much work with higher value EDO’s (and even divisions of two or more octaves) has been explored for special properties between intervals as well as other symmetric and asymmetric tuning structures. These are regularly discussed and shared in community user groups (listed below).
REFERENCES FOR FURTHER STUDY
As mentioned, this appendix would only scratch the surface of a deep and complex subject. And of course we have barely touched upon non-Western scales and tuning systems.
Xenharmonic Wiki
This is an extremely broad resource for both beginning and advanced study of tunings and temperaments, with many links to other resources. A great place to start.
Kyle Gann's Just Intonation Explained
Another excellent resource focused on JI.
Carey Beebe's Harpsichord Tuning FAQ
Excellent explanations of the historic theory and practice behind various tuning systems and their derivation.
Facebook Microtonal Music and Tuning Theory Group
An active and wide-ranging discussing of high-level tuning ideas and music created by them.
Scala
Scala is a multi-platform software package from the Huygens-Fokker that allows users to create and experiment with all types of tuning paradigms from simple to highly complex. It is capable of then outputting via MIDI (with pitch bend) to synths. Scala tunings, saved as text, can be shared and can be found as examples in some of the links above.
