Chapter One: An Acoustics Primer

15. How do we perceive pitch?
Pitch is our perceptual interpretation of frequency. As previously mentioned, ideal human hearing ranges from 20 to 20,000 Hz. Yet we have our greatest sensitivity to frequencies which lie within 200 to 2000 Hz, which takes up two-thirds of the distance on the basilar membrane. One proof of this is the just noticeable difference, or JND. The JND is the smallest change in frequency of a single sine tone that is perceptible by the average listener. Most studies place it around 3% in the 100 Hz range, but only 0.5% in the 2000 Hz range. One might extrapolate that a bass player has more liberty to play out of tune than a violinist.
The formula for successive equal temperament 12-notes-to-an-octave semitones (called 12tet) is a frequency ratio of one to the twelfth root of two (12√2 or 21/12), which approximately equals ~1:1.05946.
If you desire more accuracy, that would be 1:1.059463094359295
As an example, to find the frequency of the A# semitone above A440, multiply 440 by 1.05946 to get ~466.163. For larger intervals, the formula Pref * 2n/12 where Pref is the initial reference frequency and n is the number of semitones above it you wish to calculate, so a minor 3rd above A440 would be computed as 440 * 23/12 (or 3/12√2). This results in 440 Hz * ~1.189207 and yields a C at ~523.25116 Hz. With equal temperament then, the ratio between the same intervals are constant, regardless of their placement. In strict equal temperament, a perfect fifth, for example, has the same ratio wherever it is in the tuning system (1:1.498307), very close to the 2:3 ratio it would be in the just intonation system.
In general, we perceive pitch logarithmically in relation to frequency. Each successive octave is a doubling of the frequency of the previous one—1ƒ, 2ƒ, 4ƒ, 8ƒ, 16ƒ... Every doubling in Hz is perceived as an equivalent octave. It is thought that because a doubling of frequency causes a response at equal distance on the basilar membrane, we hear octaves as related. Do NOT expect your piano to be tuned in perfect equal temperament, however. A good tuner will stretch octaves out from the middle, dependent on the size of the piano and the inharmonicity of the strings, and squeeze or expand certain intervals inside those octaves.
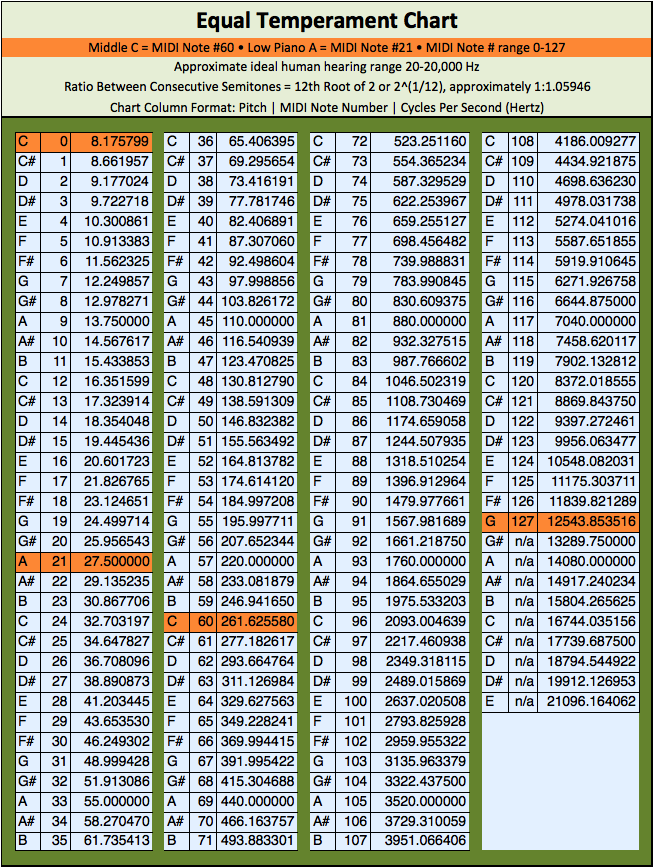
Because of the logarithmic spacing of pitch placement on the basilar membrane, we perceive musical intervals not as differences in frequency, but as ratios between frequencies. A220 to A440 is perceived as the same interval as A440 to A880, even though one pair has a frequency difference of 220 Hz and the other a frequency difference of 440 Hz because they share a 2:1 frequency ratio. Below is a chart of frequency vs. pitch, with MIDI note numbers thrown in. Click here to download as an Excel spreadsheet of the chart below for copying and pasting specific frequencies if needed.