Chapter One: An Acoustics Primer

10. What is resonance?
Resonance is characterized as the selective amplification of an external source, called the excitation source, whose frequency or frequencies match the natural vibrational characteristics of a resonating system. In musical acoustics, these systems may be strings, tubes, cavity vessels such as bottles or your vocal tract, sound boards, wooden instrument bodies, etc. Most of these resonating bodies will have multiple natural, often harmonically-related frequencies that they amplify, though some frequencies may be amplified to a greater degree than others. If an excitation source produces frequencies outside the resonating frequencies of the system, no amplification takes place, essentially filtering out those frequencies compared to those which are amplified. Acoustic resonance is a subset of mechanical resonance, which we have seen earlier in the form of spring/mass or pendulum examples, both of which have natural resonant frequencies. In reality, many instruments, such as a violin, exemplify acoustic (air-based) and mechanical (string and wood) resonance complexes that combine to give the instrument its unique characteristic sound, as the wood and air may produce a different set of resonant frequencies, exemplified by a resonance curve.

Individual Resonant Characteristics
There is much more to what makes an instrument sound like a particular instrument, or your voice sound like your voice and not your neighbor's, besides the spectral envelope of the excitation source. One such element is the unique characteristic of a particular resonating system. If you have ever stretched a string across a cardboard box and plucked it, you likely noticed the resultant timbre did not sound like a fine acoustic guitar. That is because cardboard boxes do not have the same resonating characteristics as both the material and shape of a hollow guitar body. When a guitar string is plucked, it vibrates and creates a rich spectrum of harmonic partials. The string itself is called the excitation source. The string oscillations cause the guitar body to vibrate through sympathetic vibrations, whereby a passive body is excited to vibrate by an active one. The larger vibrating surface area of the body creates higher amplitudes by causing substantially more air to move at the body's resonant frequencies. The body does not proportionately amplify all of the frequencies of the string. Instead, some frequencies are amplified more than others, giving it a unique characteristic, and indeed, different characteristics for different string pitches. It should be noted that much of the sympathetic vibration of a resonating string instrument body is transmitted to the body mechanically through the bridge and sound post, as the actual air displaced by the vibrating string is minimal.
Tubes of various diameters and lengths also have easy-to-calculate resonating frequencies, which varies depending on their shape, diameter, and openings. Tubes are capable of resonating at multiple, harmonically-related frequencies simultaneously. Whether the tube is open on both ends, or closed on one end, or cylindrical or conical in shape will also affect the resonant frequencies. The vibrating air columns set up in such resonators produce different configurations of standing waves, discussed in a later chapter. As indicated below, these tubes may be half- or quarter wavelength long depending on their openings or shape, and produce all or only odd-numbered partials. A brief chart (ignoring diameter) of these tubes and their characteristics follows:
| Type | By Tube Length (L) | By Fundamental Frequency (ƒ1) | Partials | Instrumental Examples |
|---|---|---|---|---|
| Cylinder Open Both Ends | L = λ/2 | ƒ1 = vsos/2L | all | flute, recorder, open organ pipe |
| Cylinder Closed One End | L = λ/4 | ƒ1 = vsos/4L | odd only | clarinet, brass instruments, stopped organ pipe |
| Cone Closed at One End | L = λ/2 | ƒ1 = vsos/2L | all | oboe, bassoon, sax |
| LEGEND: L=tube length, λ=wavelength,vsos=speed of sound | ||||

Cavity Resonators
Cavity resonators, such as a Coke bottle, can be excited by blowing across the opening with the right pressure and angle. These resonators have a single natural frequency that is determined by the the area of the opening, internal volume of the cavity, and the length of the neck. A larger opening gives a higher frequency, whereas greater volume and/or longer neck creates a lower frequency. As you may have experienced on a swing, a form of pendulum with a natural resonant frequency, it is difficult to force a resonator to produce something other than its natural frequency. The formula for calculating the resonant frequency of a cavity resonator is:
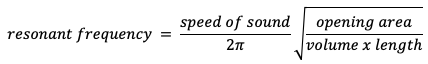
See the Hyperphysics air column reference below for further study. Recently, physical modeling and a subset, digital waveguide synthesis software has made use of physical resonator properties to artificially create similar phenomena without the physical restrictions of the real world. For example, a program might model a 200'-long flute.
For further study, see Hyperphysics->Resonance, Hyperphysics->Resonance of Air Columns