Chapter One: An Acoustics Primer

6. What is wavelength?

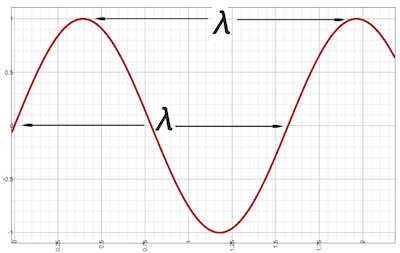
Frequency is directly related to wavelength, which is represented by the Greek symbol lambda (λ). The wavelength is the distance in space required to complete a full cycle of a traveling wave.

wavelength graph

The formula for an airborne* wavelength is:

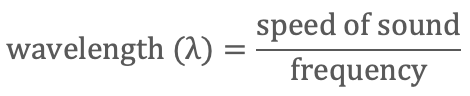
wavelength formula

Because a sound wave propagates through space at the speed of sound, calculations are done in the same units (inches, feet, meters, etc.).

Examples: an A440 Hz waveform (the frequency most modern orchestras tune to) in a dry, 20°C (68°F) room would create a wavelength that is:

~30.7 inches (≅ 13,504 inches/sec   /   440 Hz)
~2.6 feet (≅ 1128 ft/sec   /   440 Hz)
~0.8 meters (≅ 344 m/s   /   440 Hz)

Notice that if the speed of sound were to change due to temperature and/or humidity and/or conducting medium, so too would the wavelength.

The wavelength of a sound is inversely proportional to its frequency. In other words, the higher the frequency, the shorter the wavelength. For example, in our human hearing range, a 20 Hz airborne wave has a wavelength of over 56 feet, while a 20 kHz wave has a wavelength of approximately 0.7 inches.

Bell X-1
Wavelength Calculator

Enter a frequency in Hz:

Hz

The wavelength for the input frequency in air at a temperature of 20°C with 0% humidity will be approximately:

inches
centimeters
feet
meters
cubits
*For the wavelength of electromagnetic waves such as radio signals or light waves, simply substitute the speed of light (≅300,000 km/s) for the speed of sound in the above formula. Light waves, whose frequencies are in the 430–750 terahertz range are so short, they are often measured in Ångströms, which is one 10-billionth of a meter long, so way, way shorter than sound wavelengths.