Chapter One: An Acoustics Primer

2. What is Sound? | Page 3
Molecular displacement, velocity and pressure
While an overall sound wave propagates out from its origin at the speed of sound, consider the contribution of the single lowly air molecule constituent of this wave, moving first in one direction away from its origin at rest (equilibrium) and then moving in the other through its origin and out to another extreme.* What about its speed? Is it always traveling at the same speed of sound as the overall sound wave? The answer is no, it is not!
Air molecules participating in an idealized sound wave accelerate smoothly in one direction, slows down to a halt at the pressure extremes of either rarefaction or compression, and then smoothly begins to accelerate in the opposite direction much like the end-weight mass of a swinging pendulum. Inertia, as minute as it may be, prevents the molecule from suddenly switching directions at a maximum velocity. A sound wave molecule’s changing velocity is demonstrated by the BLUE cosine function on the graph below. Its oscillating position in space and the overall sound pressure at the point of the molecule is represented by the RED sine function. The molecule reaches maximum speed as it passes through its origin, and it then gradually slows to a halt as it finds itself in a denser and denser clump of molecules at maximum compression (max pressure). From there, it slowly begins to accelerate in the opposite direction, reaching maximum velocity again at its origin and begins to slow down and stop as it finds itself alone in the state of rarefaction (min pressure). And from there, it begins to accelerate towards it origin once again to continue the cycle. This is again like the swinging pendulum, whose end-weight achieves maximum velocity at what would normally be its state of rest or equilibrium were it not in motion, and whose lowest value of swinging velocity is at either extreme of its ambit.
In the graph below, note that the maximum displacement and maximum or minimum pressure correspond with the minimum of the air molecule's velocity, and that the air molecule's maximum velocity corresponds with the minimum of displacement and least amount of pressure change.
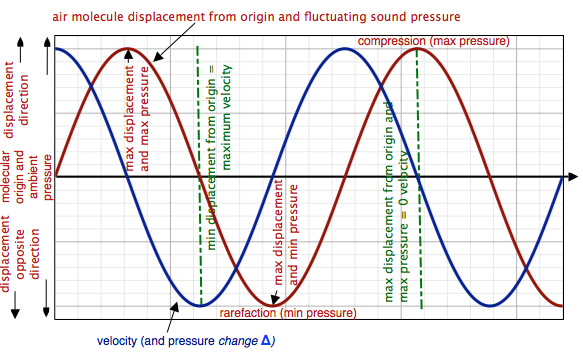
It may seem to be counter-intuitive that at the peaks and troughs of sound pressure, the molecules are not moving at all (or in the real world, moving minimally), yet they are moving the fastest at through point of minimal overall pressure change (equilibrium)! Mathematically, the above chart demonstrates that if the motion of the molecule's displacement forms a sine wave, then the corresponding molecular velocity and rate of pressure change (or pressure delta) is in a cosine relationship.
Greater maximum molecular velocities mean greater sound wave amplitude. Amplitude in sound refers to the degree of change in atmospheric pressure above or below the ambient pressure of equilibrium. The primary determinant of amplitude is the maximum velocity of individual molecules involved in the wave.

Transfer of Energy
To impart individual particle velocities to adjacent molecules, a force as a transfer of energy (what physicists call work) is required, and this often occurs across mediums. For example, a bass drum head, when struck, will impart its mechanical energy of physical oscillation to the adjacent air molecules, causing them to move to and fro as outlined above and transferring their kinetic energy to other adjacent molecules. As the sound wave propagates through space in this fashion, perhaps a small portion of it will strike your ear drum causing it to oscillate in a fashion proportional to original bass drum head. As described later in our psychoacoustics chapters, these minute ear drum movements will be converted into fluid vibrations, and converted again to electrochemical nerve signals that will communicate these pressure changes to your brain. Your brain may decide the pattern of these oscillations seems familiar, and perhaps you will say to yourself, "I think I just heard a bass drum!"
A fantastic and concise description of the relationships between sound, energy, force, work, power, amplitude, pressure and velocity at a level easily understood without extensive scientific training can be found in Mark Ballora: Essentials of Music Technology, 2003.
*The above explanation is an idealized version of reality, assuming molecules of a sound wave move reciprocally back and forth along a single axis, where as in reality, they are bumped and jostled all over the place--but this model is useful for an overall generalization of the sound pressure wave model.