Chapter One: An Acoustics Primer

8. What are wave shapes and spectral content? | Page 2
Most acoustic instruments not in the ‘noise’ category produce some combination of fundamental and harmonic partials. Bells are a category of sound that produces inharmonic partials, so called, because they do not correlate to the harmonic partials shown on the previous page.
The collection of frequencies produced by a waveform are prime contributors to its spectrum (pl. spectra). For a periodic waveform, the shape of the wave determines not only the frequency of the partials, but also their relative strength, another important factor of timbre.
In the early 19th Century, the French mathematician/physicist Jean-Baptiste Fourier (1768-1830) determined a principle, known as the Fourier series, which eventually led to methods of deconstructing complex waveforms into their component frequencies (or visa versa), known as Fourier analysis, calculated today by computers in the blink of an eye.

Fourier's Principles of Complex Periodic Waves
1) all complex periodic waves may be expressed as the sum of a series of sinusoidal waves
2) that these waves are all harmonics of the fundamental and
3) that each harmonic has its own amplitude and phase (which we have not discussed yet).
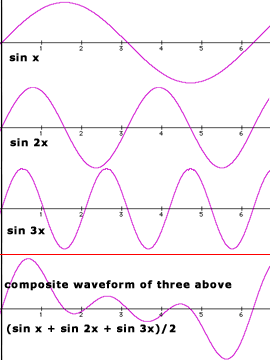
Above, summing three harmonically-related sine waves (frequencies x, 2x, and 3x) creates a single composite wave shape containing all three frequencies.
With the advent of computers and digitized audio data, it has become routine to perform Fourier analysis on existing sound to break it down into its component frequencies along with their specific amplitudes and phases. It has also become commonplace to 'reverse engineer' this process and create complex timbres by carefully mixing sine waves in a process called additive synthesis, practiced masterfully by composer Jean-Claude Risset amongst many others. A related technique called phase vocoding, used to slow down or speed up sound without changing pitch, or change pitch without changing speed, also uses Fourier analysis.