Chapter One: An Acoustics Primer
7. What is amplitude? | Page 2
Amplitude, power and intensity are correlative components of sound over time, area and distance respectively. Below, we will see how these three phenomena correspond.
Amplitude is a measurement of the magnitude of displacement (or maximum disturbance) of a medium from its resting state, as diagrammed in the peak deviation example below. It can also be a measurement of an electrical signal's increased or decreased strength above or below a nominal state. If you are watching your speaker woofer create a minute disturbance of air molecules by moving in and out a fraction of an inch from its resting state, and it suddenly starts moving in and out by several inches, you can assume that the amplitude of the sound pressure wave has increased, because the maximum disturbance of the air molecules has increased. In our discussion, we will try and minimize any confusion between mechanical or electronic measurements of amplitude, and amplitude expressed as an acoustic measure of sound pressure. Since this is an acoustics chapter, let's start with the latter.
The amplitude of sound pressure is frequently measured in pascals (Pa). One thousand pascals is a kilopascal (kPa). For reference, sea-level air pressure (1 atmosphere) is approximately 100 kPa, close to 15 pounds per square inch, and the pressure measurements we take to express amplitudes are the pressure changes above or below that equilibrium. A micropascal (μPa) is one millionth of a Pascal.
Newtons and Pascals
Causing air molecules to move in a particular direction and with a velocity other than their normal state of motion to create a sound pressure wave requires force.
One newton (N) is the amount of force it takes to accelerate a 1-kilogram object by one meter per second per second (m/s2).
One pascal (Pa) is equivalent to the pressure of one newton per square meter (N/m2).
The benchmark threshold of hearing, the smallest perceptible amplitude, is approximately 0.00002 N/m2, or 20μPa for a 1 kHz tone in laboratory conditions. 60 N/m2 (60 Pa) is considered by some to be the threshold of pain, but as we will see, this is also subjective and varies greatly by individual and age. A jack hammer at one meter's distance creates an estimated sound maximum field pressure of 2 Pa, while a jet engine at the same distance creates a maximum pressure of 632 Pa. Normal conversation may be between 0.002 and 0.2 Pa (0.2 Pa being my Aunt Frannie).
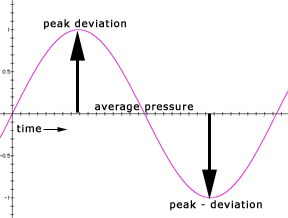
Peak Deviation
Discussions of amplitude depend largely on measurements of the oscillations in barometric pressure or electrical energy from one extreme (or peak ) to equilibrium and are not normally measured peak to peak (PP). The degree of change above OR below an imaginary center value is referred to as the peak amplitude, or peak deviation , of that waveform.
Some signals may not be symmetrical around a 0-based equilibrium, a characteristic known as DC offset or DC bias. To assess amplitude, the offset is removed before any calculation. Because such an offset may lead to unwanted amplitude-related distortion at high volumes, many audio programs include a DC-offset remover.
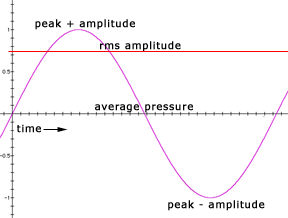
RMS
If we tried to calculate the average amplitude over time of a sine wave, it would unfortunately equal zero, since it rises and falls symmetrically above and below the zero reference. This would not tell us very much about its amplitude, since low-amplitude and high-amplitude sine waves would appear equivalent. A more meaningful reference has been developed to measure the average amplitude of a wave over time: the root-mean-square or rms method. You may also see the rms measurement applied to the power output of an amplifier.
The rms value of a waveform represents a squaring of the instantaneous amplitude for each point in time (or a sufficient number of equally spaced points) of a waveform, calculating the average (arithmetic mean) of those values, and finally taking the square root of this average.
Example: The rms of a sine wave with a hypothetical peak-to-peak value of –1 to 1 will be 0.707. This can be used to extrapolate that:
Any sine wave rms amplitude = 0.707 x peak amplitude.
Peak amplitude = 1.414 x rms amplitude.
To get the rms of a sine wave with an amplitude of 3 with 4 sample values, we would first get 0,3,0,-3 sample values. When each is squared (0,9,0,9) and then averaged (18/4), we'd get 4.5, and when we take the square root of 4.5, we'd get an rms of ~2.12. Note this is the same as multiplying the sine wave's amplitude (3) by the 0.707 rms of a 1-amp sine wave.
An ideal square wave's rms would equal its peak amplitude, since the wave is always at one peak or the other. Example: A square wave with a peak amplitude of 1 would have samples of 1, 1, -1, -1; when squared, averaged and sq root'ed, the wave would have an rms value of 1 as well as a peak amp of 1.
KNOW YOUR METERS!
When using audio gear or software, it is important to know whether your meter is a peak-reading meter or averaging meter (or neither). While there are many good reasons to keep an eye on a signal’s peaks, the rms average is far more akin to the way we hear. In the real world, most signals don't make pretty little pictures like sines, triangles or squares, and their amplitudes over time are continuously fluctuating. So rms measurements are made as a moving average where the time domain period of an averaging meter (how far back in the signal's history they look) may be selected by choosing the meter's fast response or slow response option. Once you have an understanding of dB’s described in the next pages, the markings on the meters might make more sense.
Mini-Factoid: Wind turbine efficiency is determined using a root-mean-cubed method as the cube of wind speed is proportional to the energy produced over time. As of this writing, wind turbines are still not believed to cause cancer or lower property values.
