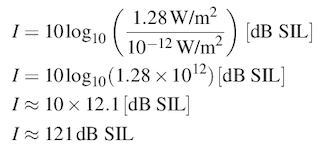Chapter One: An Acoustics Primer

7. What is amplitude? | Page 4
Decibels: Definition, decibels that measure power and intensity
While power is measured in watts, a widely-used measurement unit for relative amplitude, power, intensity, sound pressure at the listener, and comparative voltage from a microphone is the decibel (dB). Named in honor of Alexander Graham Bell, the measurement was derived from a scale originally used to determine signal loss in telegraph and telephone lines, which resulted in the bel. To mitigate fractional values of the larger bel, a decibel, which is 1/10 of a bel, became the standard. A decibel is a logarithmic measurement that reflects the tremendous range of sound intensity our ears can perceive and closely correlates to the physiology of our ears and our perception of loudness. There are many different forms of decibel measurement, and it is not always clear which method of computation is being used, although a few labels exist, and you may see such qualifiers that suggest the method or reference value, such as dBm, dBV, dB SPL, dB SIL, dB SWL, dB FS, dBu, dBVU, or even scale weightings such as dB(A) and dB(C) which we use on our sound level meters and will examine later on.
Ambiguity abounds in dB labeling, so take care you know what is being measured and the reference benchmarks being used. The SI (International System of Units), ISO and others do not recognize any of the suffixes above for decibels, and in literature, the letter 'p' is often used in dB equations to represent power, pascals or pressure, which are NOT interchangeable, so mind your 'p's' if not 'q's'.
To get started, a quick look at logarithms (often misspelled by we musicians as logarhythms) is in order.
Be not intimidated by calculating logarithms-with cheap calculators to do the math (one previously used log tables), just a simple understanding of how they work is all that is necessary for decibel calculations (if you turn your iPhone or Android phone horizontally while using the onboard calculator, it will be happy to compute complex logs for you, but just be sure to use the log10 function, not natural log (ln)).
\(\log_{10} x\) can be thought of as "what power of 10 will result in x." For example, \(\log_{10} 100 = 2\) because \(10^2 = 100\).
Decibels are often used to measure very minute values, which can also be expressed by logs of decimals numbers or their negative power equivalents e.g. \(x^{-y}\).
For example, \(\log_{10} 0.1 = -1\) and \(\log_{10}\) \(0.000000000001 = -12\) because \(10^{-12}\) = \(0.000000000001\), a value we will use for our threshold of hearing measurement below.
If a log is expressed \(y = \log_{10} x\), then \(10^y = x\).
Decibels
A decibel is a measurement used to compare the ratio of power, intensity or amplitude between two acoustic sounds or electronic signals. The ratio (R) of two signals expressed by their power in watts (W1 and W2) is:
A doubling of power equals an increase of +3 dB (try it out with the formula above). When we study filters later on, you will notice that a filter cut-off frequency is defined as the half-power point, which is calculated as –3 dB.
Decibels that measure power and intensity
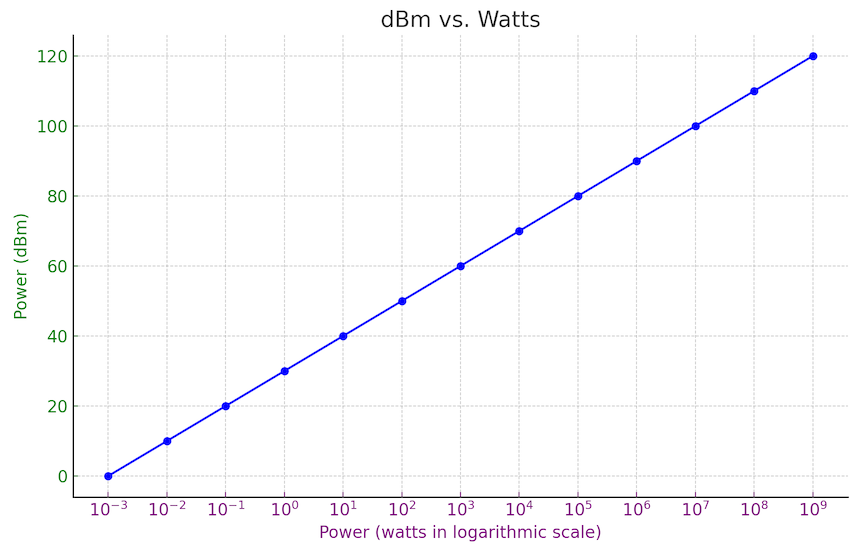
There are many different types of decibel measurements, so for the purpose of clarity, the above form, which measures power or intensity, is called dBm when a fixed reference value is used for the denominator. dBm is the form most commonly used to evaluate power in audio circuits. For the purpose of having a standardized absolute measurement of power in an electronic circuit (i.e., a comparison not to another signal, but to an industry-fixed value), the nominal reference wattage (W2) has been defined as 1 milliwatt (0.001 watt). In absolute terms, a 1-watt signal, which has 1,000 times the power of the reference wattage, will be 30 dB, computed below:
| dBm=10 log10 (1 watt/.001 watt) dBm =10 log10 (1000) dBm=10 x 3 [because log10 1000 = 3] dBm=30 |

Watts–Milliwatts–dBm calculator
Enter one of the values, click Calculate button to compute the others.
Click Reset to enter a new value.
For acoustic measurement of the total power radiated in all directions (referred to as Sound Power Level, or SWL), the same formula is used with a reference level correlating to threshold of audibility that we mentioned earlier, 10-12 watts (also called a picowatt). Note how loud a sound with 1 watt of total acoustic energy might be at 120 dB SWL—it is the reported sound of a typical jet plane at 500 feet (whaaat, those four engines produce only 1 acoustic watt of sound? Yeah.).
| dB SWL=10 log10 (1 watt/10-12 watts) dB SWL =10 log10 (1012) [that's some nifty math there] dB SWL=10 x 12 [because log10 1012 = 12] dB SWL=120 |

Acoustic Watts-Milliwatts-dB SWL Calculator
Enter one of the values, click Calculate button to compute the others.
Click Reset to enter a new value.
Since intensity (I) at a fixed distance of measurement is directly proportional to power, a similar measurement can be made for intensity using a reference value of a picowatt per meter squared or I = 10-12 W/m2 in place of Iref below to make it a Sound Intensity Level (SIL).
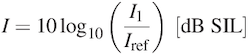
As a reminder, acoustic intensity is the measurement of power, or the rate at which energy passes through a defined area perpendicular to the direction of wave propagation. So a power measurement (watts) over an area measurement (meters2) is needed, as demonstrated below.
A real-world example of intensity measured in decibels |
As you recall from the chart on the previous page, intensity is a measure of power present over or through an area, so let's figure out the acoustic intensity in dB SIL present at the surface of a loudspeaker with a cone radius of 0.5 meters receiving 1 watt of power. As stated, the common reference level for \( I_{\text{ref}} \) is \( 10^{-12} \ \text{W/m}^2 \).* Note the example below contains some rounding for clarity. STEP 1: Find the area (A) of the speaker cone. The area of a circle is \( \pi r^2 \), so the cone area \( = \pi(0.5^2) = \pi \cdot 0.25 \approx 0.78 \) square meters. STEP 2: Compute the sound intensity in watts per meter squared by dividing the applied power of 1 watt by the cone area of 0.78 m2. So \( \frac{1}{0.78} \ \text{W/m}^2 \approx 1.28 \ \text{W/m}^2 \) gives us the sound intensity at the surface of the speaker. STEP 3: Compute the dB SIL using the STEP 2 sound intensity of \( 1.28 \ \text{W/m}^2 \) and the SIL reference value of \( 10^{-12} \ \text{W/m}^2 \) plugged into the dB SIL formula above:
So, 1 watt of power in terms of intensity I at the loudspeaker cone gives us an approximately ear-splitting 121 dB SIL, very close to the 120 dB SWL above using 1 watt signal and the picowatt reference — it would be even closer without the rounding errors. As we moved farther away from the speaker and the sound field spreads out, this measurement would change dramatically at the surface of the sound sphere as our STEP 1 area increased geometrically. BTW, you might be wondering why you'd buy a 500 watt amplifier if you can get 121 dB intensity out of a honking large speaker with only 1 watt of power. The sad fact is speakers are extremely inefficient at converting electrical power into acoustic power, so alas, only a small fraction of this energy is transferred. *Thanks to David Howard/Jamie Angus Acoustics and Psychoacoustics, 4th ed. 2009 for this example idea. |