Chapter Four: Synthesis

8. Principles of Audio-rate FM Synthesis | Page 2
Calculating sideband frequencies
Sideband frequencies can be calculated with the following formula where
Cƒ = carrier frequency, Mƒ = modulator frequency, and n = 0 and all positive integer multiples:
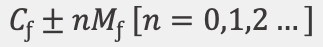
OR (in words)
the carrier frequency (Cƒ) plus and minus all the integer multiples of the modulating frequency (Mƒ) beginning with the Cƒ ± 0.
Cƒ, Cƒ + Mƒ, Cƒ - Mƒ, Cƒ + 2Mƒ, Cƒ - 2Mƒ, Cƒ + 3Mƒ, Cƒ - 3Mƒ, etc. to infinity and beyond.*
For example, a carrier frequency of 400 and a modulating frequency of 50 will produce the spectrum listed below for the first three sideband pairs (indices of n=0 to n=2)
| integer multiple index |
fm spectrum | formula to find spectrum | math to find spectrum |
|---|---|---|---|
| n=0 | 400 Hz | Cƒ ± (0 * Mƒ) | 400 + (0 * 50) |
| n=1 | 450 Hz, 350 Hz | Cƒ ± (1 * Mƒ) | 400 + (1 * 50), 400 - (1 * 50) |
| n=2 | 500 Hz, 300 Hz | Cƒ ± (2 * Mƒ) | 400 + (2 * 50), 400 + (2 * 50) |
A graph of these sideband pairs up to n = 4 looks like this:
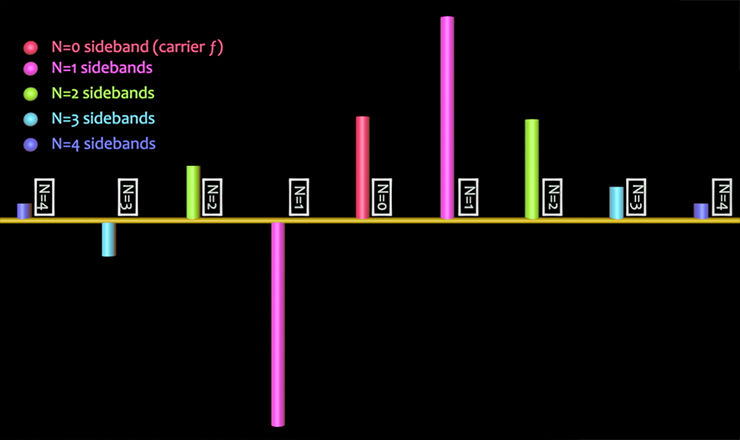
Sideband Phase
Note that the ODD number indexed pairs (n = 1,3,5, etc) have their lower sideband component in reverse phase to their positive upper sideband counterparts, indicated in the graph as the descending lines. This will become important shortly when we discuss sideband strength and reflected sidebands in the next few pages.
Carrier:Modulator (C:M) Ratio
Another method for calculating sidebands, useful when the carrier and modulator are maintaining a constant frequency relationship, is through a ratio of carrier to modulating frequency (C:M). For example, a Cƒ of 100 and an Mƒ of 200 would produce a C:M ratio of 1:2 (click here to see how to reduce C:M ratios to their normal form). We'll see later that integer ratios that have a carrier value of 1 have certain harmonic properties. It is important to note, however, that the carrier frequency is not necessarily the fundamental of a harmonic spectrum in FM, since it may not be the lowest sounding pitch produced. In the graphic example above, with Cƒ = 400 Hz and Mƒ = 50 Hz, the lowest sounding sideband is 50 Hz, which would be considered the fundamental.
*literally—FM is theoretically not band-limited and sideband frequencies might continue on up forever, where it not that they eventually lose enough strength and become insignificant past a certain point—but that is an issue for digital synthesis.