Chapter Four: Synthesis

Reflected Sidebands

What happens to the negative frequency values that we inevitably compute for lower sidebands past a certain integer multiple index (i.e. is there such a thing as a negative frequency)? Using our two methods of calculating sidebands, if we produced a carrier ƒ of 300 Hz and a modulator ƒ of 200 Hz , a 3:4 C:M ratio. If we calculate the n = 2 pair, we get an upper sideband of 700 Hz, but a lower sideband of -100 Hz, using the sideband formula on the preceding page. These sidebands in the negative domain are called reflected sidebands, because they bounce back from zero at their absolute value ,180 degrees out of phase with what their original phase would have been. So for calculating only frequency, we simply remove the minus sign, expressed mathematically as absolute or |-100|. If these frequencies do not bounce back on top of other frequencies, then the phase reversal is inaudible. However, as is particularly true in harmonic spectra, when sidebands do bounce back on top of other partials, phase cancellation or summation has a great impact on the timbre. For example, if you had a positive sideband at 400 Hz and a negative sideband at 400 Hz but half the strength of the positive one, only half the amplitude of the positive one will survive. If both were at equal strength, neither would be heard since they would completely cancel each other out. If they were both positive or both negative, they would be summed. In our example above of a C_ƒ=300 Hz and M_ƒ=200 Hz, the lower sideband of the n=2 pair would reflect back on the lower n=1 sideband. And as indices above n=2 sound, many more reflected sidebands will reflect back upon the positive sidebands with this C:M ratio. Who will survive will be a mystery to be solved below when we can calculate the relative strength of each.

Odd-indexed Reflected Sidebands or the Strange Case of the Double Negative

We had previously mentioned that odd-indexed (n=1,3,5...) lower sidebands were flipped 180° out of phase with their upper sideband counterparts. So what happens to these odd-indexed sidebands when they are reflected back from 0 Hz? They are again flipped 180° so in essence they come out in the same phase as their upper sideband counterpart, having been flipped 360°.

Harmonic vs. inharmonic spectra and finding the fundamental frequency

If C and M are both integers (N), a ratio of 1:N will be harmonic but missing the partial numbers which are multiples of N, except for 1:1. A 1:1 ratio, where the carrier and modulator are the same frequency, will include all harmonic partials. A 1:2 C:M ratio, however, will be missing all the even-numbered partials. Theoretically, any C:M ratio that is reducible to integers will produce sidebands that can be seen as harmonically related. Moreover, the reflected sidebands will reflect back on top of existing harmonic partials.

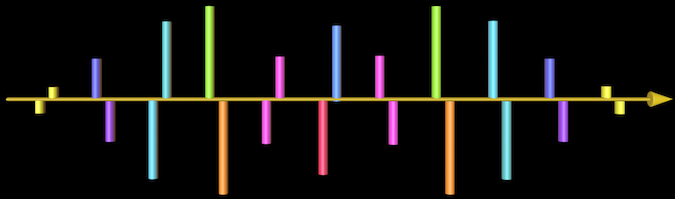
If either the carrier or modulator frequency is an irrational number (numbers cannot be written as a ratio of two integers), then the spectrum will be inharmonic. Some integer ratios are very close to irrational, such as Chowning's favorite 1:1.31 or 100:131 as integers. The result for the listener, who will not be able to fuse the sound into a harmonic one, will for practical purposes be inharmonic. The nature of these inharmonic spectra, which have at least twice the frequency components of the harmonic spectra with no phase cancellation by reflected sidebands, giving FM synthesis a wide palette of bright, vibrant timbres, including many bell-like possibilities. Many of these inharmonic spectra can have sidebands that reflect close to, but not on top of existing sidebands, providing the opportunity for shimmering, chorusing-type effects with certain ratios. Below you can see that the reflected sidebands do not reflect to positions midway between the non-reflected sidebands, thereby creating an inharmonic spectrum. A little further tweaking of the C:M ratio below could put these reflected sidebands closer to, but not directly on top of the non-reflected ones, creating a chorusing effect.

For harmonic spectra, there will usually be an implied fundamental frequency, though it may not always be audible. The carrier frequency is not necessarily the fundamental frequency. For the carrier to be the fundamental, M must be greater than or equal to 2 * C, or else be a 1:1 C:M ratio.